Langkah-langkah melukis grafik fungsi kuadrat. Menentukan 4(empat) bentuk persamaan fungsi kuadrat, yaitu melalui tiga titik yang tidak segaris, memotong sumbu x di dua titik dan melalui satu titik memotong sumbu y, melalui titik balik dan melalui satu titik memotong sumbu y, melalui titik singgung pada sumbu x dan titik potong pada sumbu y.
Rumus fungsi kuadrat:f(x) = ax2 + bx + c, dengan a ≠ 0
sumbu simetrix = -b/(2a)
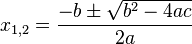 Rumus kuadratis dikenal pula dengan nama 'rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk
Rumus kuadratis dikenal pula dengan nama 'rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk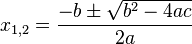
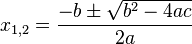
- diskriminan positif, terdapat dua titik potong antara
 dan
dan 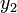 ,
, - diskriminan nol, terdapat hanya satu titik potong antara
 dan
dan 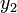 , dan
, dan - diskriminan negatif, tidak terdapat titik potong antara kedua kurva,
 dan
dan 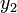
- diskriminan positif, terdapat dua titik potong antara
 dan
dan 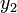 ,
, - diskriminan nol, terdapat hanya satu titik potong antara
 dan
dan 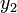 , dan
, dan - diskriminan negatif, tidak terdapat titik potong antara kedua kurva,

- Jika dikriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional — sebaliknya dapat pula merupakan bilangan irrasional kuadrat.
- Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah:

- Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:
 dan
dan 
- Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilaitidak negatif.
Akar riil dan kompleks
Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagaititik potongnya dengan sumbu x atau garis y = 0.
Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.Titik potong dengan garis y = d
Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadratdengan suatu garis mendatar
- Intepretasi yang sama pun berlaku, yaitu bila:
- diskriminan positif, terdapat dua titik potong antara
 dan
dan 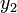 ,
, - diskriminan nol, terdapat hanya satu titik potong antara
 dan
dan 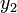 , dan
, dan - diskriminan negatif, tidak terdapat titik potong antara kedua kurva,
 dan
dan 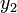 .
. Nilai-nilai y
Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai yberharga positif atau negatif. Harga-harga ini ditentukan pula oleh nilai konstanta kuadrat a:
Harga-harga y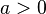 0\!">
0\!">
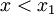

 x_2\!">
x_2\!">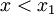

 x_2\!">
x_2\!">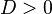 0\!">
0\!"> 0\!">
0\!">
 0\!">
0\!">
 0\!">
0\!">
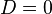
 0\!">
0\!">
 0\!">
0\!">


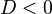
 0\!">
0\!">
 0\!">
0\!">


- diskriminan positif, terdapat dua titik potong antara
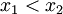 merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila
merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila 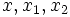 bersifat kompleks, maka yang dimaksud adalah
bersifat kompleks, maka yang dimaksud adalah 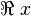 (nilai riil)-nya.
(nilai riil)-nya.













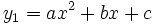

nee nie almat blogspot q.............xie greenas,,
BalasHapusnee q mnta almt blogspotnya puji,
krim blik e0w...
thag tunggu,,
by:greenas,,IPS 1
ada kug di blogku
BalasHapus